Question

Find an equation of the tangent line to y = 2e^x sec(x) at x = pi/4

Answer 1

y = 6.20 + 12.4(x - pi/4)

Explanation:

dy/dx = 2e^x secx + 2e^x secx * tanx= 2e^x secx (1 + tanx)

At x = pi/4, use sec(pi/4) =
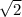`√(2)`. tan(pi/4) =1

so dy/dx = 2e^(pi/4) *
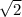`√(2)` * (1 + 1) =
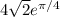`4 √(2) e^(\pi/4)` ≈ 12.4 (This is the slope of the tangent line)

When x = pi/4, y = 2e^(pi/4) *
`√(2)` =
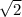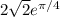`2 √(2) e^(\pi/4)`= 6.20

Then the equation of the tangent line is

y = 6.20 + 12.4(x - pi/4)