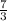Answer:
y=
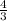 x+
x+
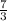
Explanation:
-3x-4y=12
1. First we need to get the equation in the form of y=mx+c to do this we add 3x to both sides and then divide it by -4 on each side to get
(add 3x to both sides) = -4y=3x+12
(divide each side by -4)= y= -
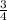 x -3
x -3
2. to find the perpendicular gradient we find the reciprocal of the original gradient
the reciprocal of -
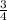 is
is
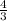
3. we can check this by multiplying them and seeing of we get -1
-
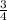 x
x
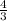 = = -1
= = -1
4. we then sub in the gradient
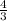 in y=mx+c this gives us
in y=mx+c this gives us
y=
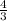 x +c
x +c
5. to find the value of c we substitute the coordinates into the equation to get ( we do this by expanding the brackets and getting c on it own)
-3=
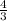 (-4) +c
(-4) +c
-3= -
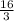 +c
+c
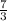 =c
=c
6. we sub
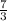 =c back into y=
=c back into y=
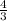 x +c this gives us
x +c this gives us
y=
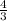 x +
x +
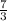
7. Therefore our final answer is
y=
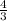 x +
x +