Answer:
2x² +5
Explanation:
You want the width of a rectangle with a length of x+3 and an area of A(x) = 2x³ +6x² +5x +15.
Area
The area is the product of length and width, so the width will be ...
A = LW
W = A/L = (2x³ +6x² +5x +15)/(x +3)
The cubic expression can be factored by grouping, so we have ...
Area = (2x³ +6x²) +(5x +15)
= 2x²(x +3) +5(x +3)
= (2x² +5)(x +3)
Then the width is ...
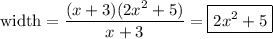
The width of the rectangle is 2x² +5.
<95141404393>