Question

Consider a set of cards that has four cards labeled 1, 3, 5, and 7. Suppose you pick two cards, without replacement, and obtain the mean of the two numbers that are drawn from the set. Which of the following tables shows the sampling distribution? a.) Sample (n = 2) x̄ S1 = {1, 1} 1 S2 = {1,This problem has been solved!You'll get a detailed solution from a subject matter expert that helps you learn core concepts.Consider a set of cards that has four cards labeled 1, 3, 5, and 7.Suppose you pick two cards, without replacement, and obtain the mean of the two numbers that are drawn from the set

Answer 1

one 2

one 3

two 4's

one 5

one 6

Explanation:

We can use the combination formula to derive how many sets of two can be obtained from this set of 4 numbers. We are using the combination formula instead of the permutation formula because, in this situation, order doesn't matter; the mean of 1 and 3 is the same as the mean of 3 and 1.

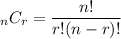`_nC_r = (n!)/(r!(n-r)!)` where
`n` is the number of things to choose from and
`r` is the number of things we are choosing. Hence the equation for this problem is:

`_4C_2 = (4!)/(2!(4-2)!)`

`_4C_2=(24)/(2(2))`

`_4C_2 = 6`

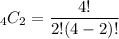
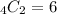
So, there are 6 ways to pick 2 cards from a total of 4. We can lay out these 6 possibilities from the given numbers on each card:

(1, 3) (3, 5) (5, 7)

(1, 5) (3, 7)

(1, 7)

Then, we can calculate the mean, or average, of each.

2 4 6

3 5

4

Finally, we can conclude that the distribution of the means for each possible set of number pairs is:

one 2

one 3

two 4's

one 5

one 6