Explanation:
Let use have a interger,n
Thus three consectice intergers can be represented by
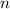

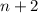
Multiply, and we get
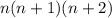
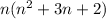
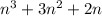
Then add the middle number, n+1.
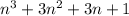
We must prove that the middle number cubed = the equation.
Using the binomial theroem,
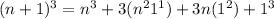
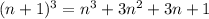
So this is indeed true.
You can do the subsitue variables for n to prove it.