Question

determine how long it will take for 650 mg of a sample of chromium-51, which has a half life of about 28 days, to decay to 200 mg. Use N(t)=N0e-kt

Answer 1

47.6 days

Explanation:

Given formula:

`N(t)=N_0e^(-kt)`

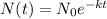
where:

• N₀ = initial mass (at time t = 0)
• N = mass (at time t)
• k = a positive constant
• t = time (in days)

First, find the decay constant (k) for chromium-51.

Given its half-life is about 28 days:

`\implies (1)/(2)=1e^(-28k)`

`\implies (1)/(2)=e^(-28k)`

`\implies \ln (1)/(2)= \ln e^(-28k)`

`\implies \ln1 - \ln 2= -28k \ln e`

`\implies -\ln 2= -28k`

`\implies k=(-\ln 2)/(-28)`

`\implies k=(1)/(28)\ln 2`

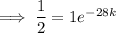
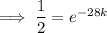
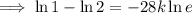
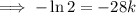
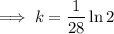
To determine how long it will take for a 650 mg of a sample of chromium-51 to decay to 200 mg, substitute the following values into the formula and solve for t:

• N₀ = 650 mg
• N = 200 mg
• 
  `k= (1)/(28)\ln 2`

`\implies 200=650e^{(-(1)/(28)t\ln 2)}`

`\implies (200)/(650)=e^{(-(1)/(28)t\ln 2)}`

`\implies (4)/(13)=e^{(-(1)/(28)t\ln 2)}`

`\implies \ln (4)/(13)=\ln e^{(-(1)/(28)t\ln 2)}`

`\implies \ln (4)/(13)=-(1)/(28)t\ln 2\ln e`

`\implies \ln (4)/(13)=-(1)/(28)t\ln 2`

`\implies -28 \ln (4)/(13)=t\ln 2`

`\implies t=(-28 \ln (4)/(13))/(\ln 2)`

`\implies t=47.61231211`

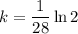
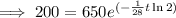
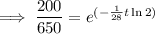
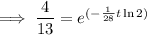
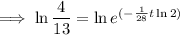
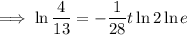
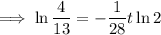
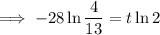
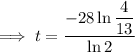
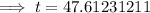
Therefore, it will take 47.6 days (nearest tenth) for a 650 mg of a sample of chromium-51 to decay to 200 mg.