Question

An electric motor is used to run an elevator. The total mass of the elevator car and passenger is 1600 kg. The elevator moves upward a distance of 15.0 m in 8.82 s at a constant speed. What is the power output of the motor during this time?

Answer 1

Approximately
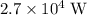`2.7 * 10^(4)\; {\rm W}`, assuming that
`g = 9.81\; {\rm m\cdot s^(-2)}`

Step-by-step explanation:

The weight of the elevator is:

`\begin{aligned}& \text{weight} \\ =\; & m\, g \\ =\; & 1600\; {\rm kg} * 9.81\; {\rm m \cdot s^(-2)} \\ \approx\; & 15700\; {\rm N}\end{aligned}`.

Since the speed of the elevator is constant, the acceleration of this elevator would be
`0`.

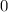By Newton's Second Law of Motion, the net force on the elevator (proportional to acceleration) would also be
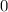`0\!`. All external forces on the elevator need to be balanced in every direction.

The only two vertical forces on the elevator are:

• the weight of the elevator (downward gravitational pull from the earth,) and
• the upward pull from the motor.

These two forces need to balance one another. Since the weight of the elevator is approximately
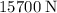`15700\; {\rm N}`, the upward pull of the motor would be
`15700\; {\rm N}\!`. in magnitude.

The direction of this upward pull is the same as the direction of the motion of this elevator. Thus, the work that the motor did on the elevator would be positive:

`\begin{aligned}& \text{work} \\ =\; & F\, s \\ \approx\; & 15700\; {\rm N} * 15.0\; {\rm m} \\ \approx\; & 2.35 * 10^(5)\; {\rm J}\end{aligned}`.

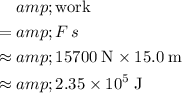Since the velocity of the elevator is constant, instantaneous power output of the motor would be equal to the average power of the motor:

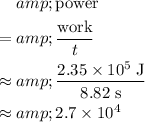`\begin{aligned}& \text{power} \\ =\; & \frac{\text{work}}{t} \\ \approx\; & \frac{2.35 * 10^(5)\; {\rm J}}{8.82\; {\rm s}} \\ \approx\; & 2.7 * 10^(4)\end{aligned}`.