Solution :
Let
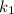 = number of levels for the factors 'flavors' = 4
= number of levels for the factors 'flavors' = 4
(4 levels vanilla, chocolate, red velvet and marbled)
The degree of freedom for the factor 'flavors' =
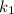 - 1
- 1
= 4 - 1
= 3
Now defining the F test statistics for testing the significance of the factors, 'flavors' :
F test statics =
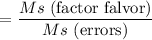 , Ms = mean square
, Ms = mean square
where F =
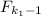 , error df.
, error df.
Thus the numerator degrees of the freedom for the F test statistics to determine if the factor flavor was significant is =
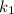 - 1
- 1
= 4 - 1
= 3