Answer:
a) 0.1496 = 14.96% probability that the demand will exceed 190 cfs during the early afternoon on a randomly selected day.
b) Capacity of 252.6 cubic feet per second
Explanation:
Exponential distribution:
The exponential probability distribution, with mean m, is described by the following equation:
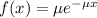
In which
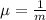 is the decay parameter.
is the decay parameter.
The probability that x is lower or equal to a is given by:
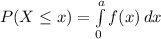
Which has the following solution:
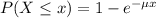
The probability of finding a value higher than x is:
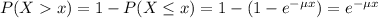
The operator of a pumping station has observed that demand for water during early afternoon hours has an approximately exponential distribution with mean 100 cfs (cubic feet per second).
This means that
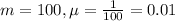
(a) Find the probability that the demand will exceed 190 cfs during the early afternoon on a randomly selected day. (Round your answer to four decimal places.)
We have that:
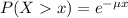
This is P(X > 190). So
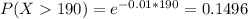
0.1496 = 14.96% probability that the demand will exceed 190 cfs during the early afternoon on a randomly selected day.
(b) What water-pumping capacity, in cubic feet per second, should the station maintain during early afternoons so that the probability that demand will exceed capacity on a randomly selected day is only 0.08?
This is x for which:
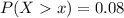
So
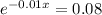
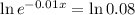
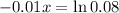
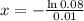
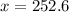
Capacity of 252.6 cubic feet per second