Question

Sphere B of charge +8q is at a distance a to the left of sphere A, and sphere C of charge +2q is to the right of sphere A.

What must be the distance from sphere A to sphere C on the right such that the original small sphere remains at rest?

Answer 1

The distance from sphere A to sphere C on the right such that the original small sphere remains at rest is a/2

Step-by-step explanation:

The force of a charge at a point is given as follows;

From an online source, we have;

E₁ + E₂ = 0

The electric field due to the sphere B of charge +8q = E₁

`E_1 = (k \cdot (8 \cdot Q))/(a^2)`

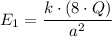
The position of the sphere B = A distance 'a' to the left of 'A'

The electric field due to the sphere C of charge +2q = E₂

The position of the sphere C = A distance to the right of 'A'

Therefore, for the electric field strength of sphere 'B' at 'A', we have;

`E_1 = (k \cdot (8 \cdot Q))/(a^2) = 4 * (k \cdot (2 \cdot Q))/(a^2)`

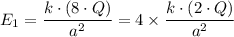
Let 'x' be the distance of the +2q charge to the right of 'A', we have;

`E_2 = (k \cdot (2 \cdot Q))/(x^2)`

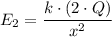
Therefore, for the force of the +2q charge to balance the +8q charge at C, we have;

`(k \cdot (2 \cdot Q))/(x^2) = (k \cdot (8 \cdot Q))/(a^2) = 4 * (k \cdot (2 \cdot Q))/(a^2)`

`\therefore \ (1)/(x^2) = (4)/(a^2)`

`\therefore \ \sqrt{ (1)/(x^2) }= \sqrt{(4)/(a^2)}`

`(1)/(x) = (2)/(a)`

`x= (a)/(2)`

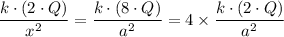
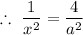
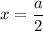
Therefore, the distance, 'x', from sphere A to sphere C on the right such that the original small sphere remains at rest is x = a/2.