Question

Seas and Colleen are raking leaves in their yard. Working together they can clear the yard of leaves in 24 minutes. What kind of long it would take Sean 20 minutes longer to clear the yard dinner with Colleen working alone

Answer 1

Colleen alone to clear the yard of leaves in 40 minutes

Explanation:

P.S - The exact question is -

Given - Seas and Colleen are raking leaves in their yard. Working together they can clear the yard of leaves in 24 minutes. What kind of long it would take Sean 20 minutes longer to clear the yard dinner with Colleen working alone

To find - When c is the number of minutes it would take Colleen to finish the job when working alone, the situation is modeled by this rational equation: How long would it take Colleen alone to clear the yard of leaves?

Proof -

Given that the equation is -

`(1)/(c) + (1)/(c+20) = (1)/(24) \\(c + 20 + c)/(c(c+20)) = (1)/(24)\\(2c + 20)/(c^(2) +20c) = (1)/(24)\\24(2c + 20) = c^(2) +20c\\48c + 480 = c^(2) +20c\\28c + 480 = c^(2)\\c^(2) - 28c - 480 = 0\\c^(2) - 40c + 12c - 480 = 0\\c(c - 40) + 12(c - 40) = 0\\(c+12)(c-40) = 0\\c = -12, 40`

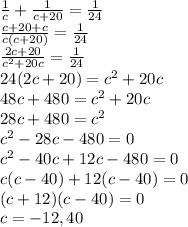
As time can not be negative

So,

we get

c = 40 minutes

∴ we get

Colleen alone to clear the yard of leaves in 40 minutes