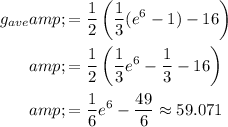Question

Find the average value of a function

Answer 1

The average value of g is:

`\displaystyle g_(ave)=(1)/(6)e^6-(49)/(6)\approx 59.071`

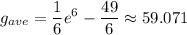
Explanation:

The average value of a function is given by the formula:

`\displaystyle f_(ave)=(1)/(b-a)\int_a^b f(x)\, dx`

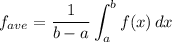
We want to find the average value of the function:

`g(x)=e^(3x-3)-4x`

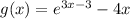
On the interval [1, 3].

So, the average value will be given by:

`g_(ave)=\displaystyle (1)/(3-1)\int_1^3 e^(3x-3)-4x\, dx`

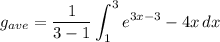
Simplify. We will also split the integral:

`\displaystyle g_(ave)=(1)/(2)\left(\int_1^3e^(3x-3)\, dx-\int _1^3 4x\, dx\right)`

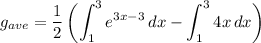
We can use u-substitution for the first integral. Letting u = 3x - 3, we acquire:

`\displaystyle u=3x-3\Rightarrow du = 3\, dx\Rightarrow (1)/(3) du=dx`

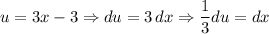
We will also change the limits of integration for our first integral. So:

`u(1)=3(1)-3=0\text{ and } u(3)=3(3)-3=6`

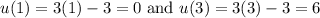
Thus:

`\displaystyle g_(ave)=(1)/(2)\left((1)/(3)\int_0^6 e^(u)\, du-\int _1^3 4x\, dx\right)`

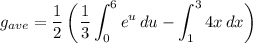
Integrate:

`g_(ave)=\displaystyle (1)/(2)\left((1)/(3)e^u\Big|_0^6-2x^2\Big|_1^3\right)`

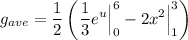
Evaluate. So, the average value of g on the interval [1, 3] is:

`\displaystyle g_(ave)=(1)/(2)\left((1)/(3)\left[e^6-e^0\right]-\left[2(3)^2-2(1)^2\right]\right)`

Evaluate:

`\displaystyle\begin{aligned} g_(ave)&=(1)/(2)\left((1)/(3)(e^6-1)-16\right)\\&=(1)/(2)\left((1)/(3)e^6-(1)/(3)-16\right)\\&=(1)/(6)e^6-(49)/(6)\approx59.071\end{aligned}`