Question

A study of 420,027 cell phone users found that 133 of them developed cancer of the brain or nervous system. Prior to this study of cell phone​ use, the rate of such cancer was found to be ​0.0414% for those not using cell phones. Complete parts​ (a) and​ (b). a. Use the sample data to construct a ​90% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system.

Answer 1

Answer: (0.00027144, 0.00036176)

Explanation:

The sample proportion of cell phone users who develop cancer of the brain or nervous system =
`(133)/(420027)=0.0003166`

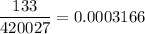
Sample size : 420027

Confidence interval for p:
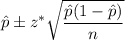`\hat{p}\pm z^*\sqrt{\frac{\hat{p}(1-\hat{p})}{n}}`, where
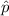`\hat{p}`= sample proportion , n= sample size , z* = crirical z value.

For 90% confidence interval , z*= 1.645

Required confidence interval:

`0.0003166\pm (1.645)\sqrt{(0.0003166(1-0.0003166))/(420027)}\\\\=0.0003166\pm 0.00004516\\\\=(0.0003166-0.00004516,\ 0.0003166+ 0.00004516)\\\\=(0.00027144, \ 0.00036176)`

A ​90% confidence interval estimate of the percentage of cell phone users who develop cancer of the brain or nervous system = (0.00027144, 0.00036176)