Question

Valeria invested $770 in an account paying an interest rate of 53% compounded

monthly. Zoey invested $770 in an account paying an interest rate of 5%
compounded continuously. To the nearest dollar, how much money would Zoey have
in her account when Valeria's money has tripled in value?
4

Answer 1

`\$856.03`

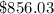
Explanation:

Continuous Compound Interest Formula:

The Continuous Compound Interest Formula is derived from the Compound Interest Formula:
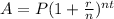`A = P(1 + (r)/(n))^(nt)`, as the number of times interest is applied, goes to infinity. Through some simple algebraic manipulation, we get the formula:
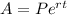`A = Pe^(rt)` (e is known as Euler's Number and is notation for a constant value like
`\pi`)

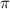Calculating Time:

Since Valeria invested 770 in an account with an interest of 53% paying monthly, we want to find how much time it takes to triple her money, and then plug that into Zoey's equation.

So let's generally solve for time in the equation:

`A = P(1 + (r)/(n))^(nt)`

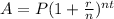
First divide by P

`(A)/(P) = (1 + (r)/(n))^(nt)`

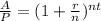
From here, it helps to take the base 10 log of both sides, so we can apply logarithmic properties, in this case we want to bring the exponent down.

`log((A)/(P)) = nt * log(1 + (r)/(n))`

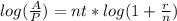
Now from here' lets divide both sides by the log (the one on the right side) and "n" to give us:

`(log((A)/(P)))/(n * log(1 + (r)/(n))) = t`

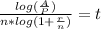
Now whenever we need to calculate time, we simply need to plug in these values. We're given the following information from the problem:

`P = 770\\r = 0.53\\n = 12\text{ compound monthly means 12 per year}\\A= 2,310 \text{ this is just 770 * 3, since we're looking for when Valeria's money triples}`

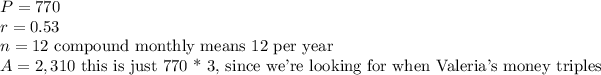
Plugging in the values we get:

`(log((2310)/(770)))/(12*log(1+(0.53)/(12))=t`

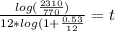
Plugging this into a calculator, gives an approximate value of:

`2.1183\approx t`

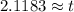
Calculating Zoey's Balance:

From here we simply need to plug values into the continuous compound interest formula:
`A=Pe^(rt)`

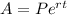
We're given the following information:

`A = 770\\r= 0.03\\`

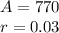
and we know that:

`t\approx 2.1183`

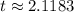
since we solved for that.

So now let's just plug values into the equation!

`A\approx 770 * e^(0.05 * 2.1183)\\A \approx 856.03`

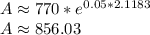
So now we have our solution!