1.

2.
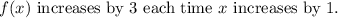
3.

1. When x = 0, the value of f(x) is:
To find the value of
 when
when
 , substitute
, substitute
 into the equation. From the point (0, -5), we get
into the equation. From the point (0, -5), we get
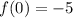 .
.
2. Each time x increases by 1, f(x) increases by:
The slope of the line
 represents the rate of change of
represents the rate of change of
 concerning
concerning
 . From the given points (3, 4) and (0, -5), we can calculate the slope as
. From the given points (3, 4) and (0, -5), we can calculate the slope as
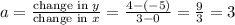 . Therefore, each time
. Therefore, each time
 increases by 1,
increases by 1,
 increases by 3.
increases by 3.
3. Write an equation to model the function:
The equation for the line in slope-intercept form is
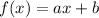 . Substituting the slope
. Substituting the slope
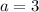 and using the point (0, -5) to find the y-intercept, we get
and using the point (0, -5) to find the y-intercept, we get
 .
.