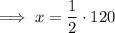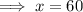Question

The measures of the acute angles in the isosceles trapezoid are one-half times the measures of the obtuse angles. Write and solve a system of equations to find the measures of all the angles.

Answer 1

`\textsf{System of equations: \quad }\begin{cases}x=(1)/(2)y\\\\2x+2y=360\end{cases}`

`\begin{aligned} \textsf{Solutions}: \quad x &= 120^(\circ)\\y &= 60^(\circ)\end{aligned}`

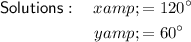
Explanation:

An obtuse angle is greater then 90° and less than 180°.

An acute angle is less than 90°.

Therefore, from inspection of the given diagram:

• x = obtuse angle
• y = acute angle

If the measures of the acute angles are one-half times the measures of the obtuse angles:

`\implies x=(1)/(2)y`

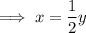
Angles in a quadrilateral sum to 360°.

`\implies 2x+2y=360`

Therefore, the system of equations is:

`\begin{cases}x=(1)/(2)y\\\\2x+2y=360\end{cases}`

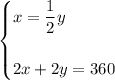
Substitute the first equation into the second equation and solve for y:

`\implies 2\left((1)/(2)y\right)+2y=360`

`\implies y+2y=360`

`\implies 3y=360`

`\implies (3y)/(3)=(360)/(3)`

`\implies y=120`

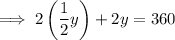
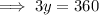
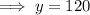
Substitute the found value of y into the first equation and solve for x:

`\implies x=(1)/(2) \cdot 120`

`\implies x=60`