Question

Gavin deposited $12,000 at 2% interest mounted quarterly what is the value after 16 years round to the nearest cent

Answer 1

final amount = $16512.36

Explanation:

The question asks us to find the value of Gavin's deposit of $12,000 after 16 years, given that the interest rate of 2% is compounded quarterly.

To do this, we have to use the following formula for compound interest:

`\boxed{A = P(1 + (r)/(n))^(nt)}`,

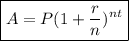where:

A → amount at the end

P → principal (original) amount

r → interest rate (in decimal)

n → number of times per year that the interest is compounded

t → time (in years).

From the question, we know that the initial amount deposited is $12,000. Therefore, P = 12000. We also know that the interest rate is 2%, but the formula requires the rate to be in decimal, so r = 0.02. The time for which the money is deposited is 16 years, and therefore, t = 16. We are told that the interest is compounded quarterly, that is, every 3 months. This means that the interest is compounded 4 times yearly, so n = 4.

From the above information and formula, we can calculate the final amount:

`A = P(1 + (r)/(n))^(nt)`

⇒
`A = 12000(1 + (0.02)/(4))^(4 * 16)`

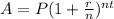
⇒ A = $16512.36

Therefore, the final amount after 16 years is $16512.36.