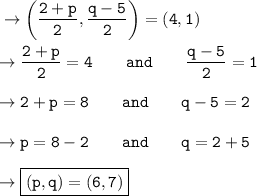Question

Given that the four points A(1,2), B(2, -5), C(7,0) and D(p,q) are the vertices of the rhombus ABCD

calculate

a) the value of p and of q​

Answer 1

Explanation:

Three coordinates of a Rhombus is given to us. And the fourth coordinate is D(p,q) . Weneedtofind the value of p and q . We know that the diagonals of Rhombus bisect each other at right angles . So lets find the midpoint.

• Midpoint of AC :-

`\tt\to Midpoint_((AC))= \bigg((x_1+x_2)/(2),(y_1+y_2)/(2)\bigg)\\\\\tt\to Midpoint_((AC))= \bigg( (1+7)/(2),(2+0)/(2)\bigg)\\\\\tt\to Midpoint_((AC))= \bigg((8)/(2),(2)/(2)\bigg)\\\\\tt\to \boxed{\orange{\tt Midpoint_((AC))= (4,1)}}`

_______________________________

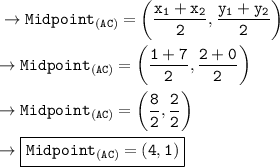
• Midpoint of BD :-

`\tt\to Midpoint_((BD))= \bigg((x_1+x_2)/(2),(y_1+y_2)/(2)\bigg)\\\\\tt\to \boxed{\orange{\tt Midpoint_((BD))= \bigg( (2+p)/(2),(q-5)/(2)\bigg)}}`

_______________________________

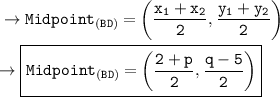
Now since these two coordinates must be equal, therefore ,

`\tt\to \bigg( (2+p)/(2),(q-5)/(2)\bigg)= (4,1)\\\\\tt\to (2+p)/(2)=4 \qquad and \qquad (q-5)/(2)=1 \\\\\tt\to 2 + p = 8 \qquad and \qquad q-5 = 2 \\\\\tt\to p = 8 -2 \qquad and \qquad q = 2 +5 \\\\\tt\to\boxed{\orange{\tt (p,q) = (6,7) }}`