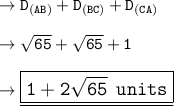Question

Find the perimeter of the polygon with vertices of the triangle A(-2, 4), B (3, 4), and C (3, -4) answer quickly​. a b and c aren't answer choices​

Answer 1

Explanation:

Three coordinates of triange are given to us and we need to find its perimeter . We know that perimeter is the sum of all sides . Lets find the distance between each sides using distance formula .

• Distance between A and B :-

`\tt\to D_((AB)) =√((x_2-x_1)^2+(y_2-y_1)^2)\\\\\tt\to D_((AB)) =√((3-2)^2+(4-4)^2)\\\\\tt\to D_((AB)) =√(( 1^2+0^2 )) \\\\\tt\to D_((AB)) =√(1) \\\\\tt\to \boxed{\orange{\tt D_((AB)) = 1\ units }}`

_________________________________

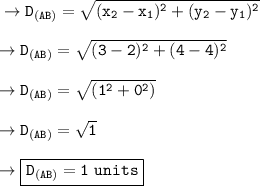
• Distance between A and C :-

`\tt\to D_((AC)) =√((x_2-x_1)^2+(y_2-y_1)^2)\\\\\tt\to D_((AC)) =√((3-2)^2+(4+4)^2)\\\\\tt\to D_((AC)) =√(( 1^2+8^2 )) \\\\\tt\to D_((AC)) =√(65) \\\\\tt\to \boxed{\orange{\tt D_((AC)) = √(65)\ units }}`

_________________________________

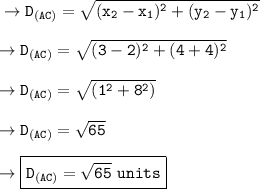
• Distance between C and B :-

`\tt\to D_((CB)) =√((x_2-x_1)^2+(y_2-y_1)^2)\\\\\tt\to D_((CB)) =√((3-3)^2+(4+4)^2)\\\\\tt\to D_((CB)) =√(( 8^2+0^2 )) \\\\\tt\to D_((CB)) =√(65) \\\\\tt\to \boxed{\orange{\tt D_((CB)) = √(65)\ units }}`

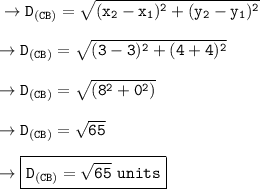
Hence the total perimeter will be ,

`\to\tt D_((AB))+D_((BC))+D_((CA))\\\\\tt\to √(65)+√(65)+1 \\\\\tt\large\to\underline{\boxed{\green{\tt 1 +2√(65) \:\:units }}}`