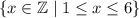Question

Need help asap please!

Answer 1

`\textsf{$f(1) = \boxed{1}$ , meaning when a $\boxed{1}$ is rolled on the die, the player is awarded}\\\\ \textsf{ $\boxed{1}$ point. This interpretation $\boxed{\sf makes \; sense}$ in the context of the problem.}`

`\textsf{$f(4.5) = \boxed{8}$ , meaning when a $\boxed{4.5}$ is rolled on the die, the player is awarded} \\\\ \textsf{ $\boxed{8}$ points. This interpretation $\boxed{\sf does \; not \; make \; sense}$ in the context of the problem.}`

`\textsf{$f(10) = \boxed{19}$ , meaning when a $\boxed{10}$ is rolled on the die, the player is awarded} \\\\ \textsf{ $\boxed{19}$ points. This interpretation $\boxed{\sf does \; not \; make \; sense}$ in the context of the problem.}`

`\textsf{Based on the observations above, it is clear that an appropriate domain for the}\\\\ \textsf{function is $\boxed{ \{1, 2, 3, 4, 5, 6\}}$ .}`

Explanation:

Given function:

`f(x)=2x-1`

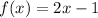
where:

• x is the value rolled on the six-sided die.
• The sides of the die are labelled 1 to 6.

----------------------------------------------------------------------------------------------------

f(1) means the value of the function when x = 1.

Therefore, substitute x = 1 into the given function to find f(1):

`\begin{aligned}x=1 \implies f(1)&=2(1)-1\\&=2-1\\&=1\end{aligned}`

`\textsf{$f(1) = \boxed{1}$ , meaning when a $\boxed{1}$ is rolled on the die, the player is awarded}\\\\ \textsf{ $\boxed{1}$ point. This interpretation $\boxed{\sf makes \; sense}$ in the context of the problem.}`

----------------------------------------------------------------------------------------------------

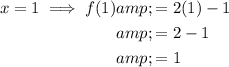
f(4.5) means the value of the function when x = 4.5.

Therefore, substitute x = 4.5 into the given function to find f(4.5):

`\begin{aligned}x=4.5 \implies f(4.5)&=2(4.5)-1\\&=9-1\\&=8\end{aligned}`

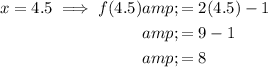
As the faces of the six-sided die are labelled 1 to 6, the only values of x that make sense are 1, 2, 3, 4, 5 and 6. Therefore, rolling a "4.5" does not make sense.

`\textsf{$f(4.5) = \boxed{8}$ , meaning when a $\boxed{4.5}$ is rolled on the die, the player is awarded} \\\\ \textsf{ $\boxed{8}$ points. This interpretation $\boxed{\sf does \; not \; make \; sense}$ in the context of the problem.}`

----------------------------------------------------------------------------------------------------

f(10) means the value of the function when x = 10.

Therefore, substitute x = 10 into the given function to find f(10):

`\begin{aligned}x=10 \implies f(1)&=2(10)-1\\&=20-1\\&=19\end{aligned}`

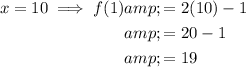
As the faces of the six-sided die are labelled 1 to 6, the only values of x that make sense are 1, 2, 3, 4, 5 and 6. Therefore, rolling a "10" does not make sense.

`\textsf{$f(10) = \boxed{19}$ , meaning when a $\boxed{10}$ is rolled on the die, the player is awarded} \\\\ \textsf{ $\boxed{19}$ points. This interpretation $\boxed{\sf does \; not \; make \; sense}$ in the context of the problem.}`

----------------------------------------------------------------------------------------------------

The domain of a function is the set of all possible x-values.

As the faces of the six-sided die are labelled 1 to 6, the only possible values of x are 1, 2, 3, 4, 5 and 6.

`\textsf{Based on the observations above, it is clear that an appropriate domain for the}\\\\ \textsf{function is $\boxed{ \{1, 2, 3, 4, 5, 6\}}$ .}`

The domain can also be written as:

`\{x \in \mathbb{N} \; | \; 1 \leq x \leq 6 \}`

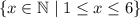
or
`\{x \in \mathbb{Z} \; | \; 1 \leq x \leq 6 \}`