Question

In two or more complete sentences, explain how to use ordered pairs of points in f(x) = 2x + 5 and g(x)= x-5/2 to determine if f(x) and g(x) are inverses of each other. PLEASE EXPLAIN WITH WORDS IN TWO SENTENCES I NEED HELP ASAP

Answer 1

See below.

Explanation:

The given functions f(x) and g(x) are linear functions. Therefore, their inverses are a reflection about the line y = x.

The mapping rule for reflecting a point about the line y = x is:

• (x, y) → (y, x)

To determine if f(x) and g(x) are inverses of each other:

• Input the x-value of the ordered pair into one function.
• Input the y-value of the ordered pair as the x-value of the other function.

If the y-value of one function equals the x-value of the other function (and the x-value of one function equals the y-value of the other function), the functions are inverses of each other.

Given functions:

`\begin{cases}f(x) = 2x+5\\\\g(x)=(x-5)/(2) \end{cases}`

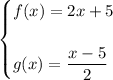
Ordered pair: (2, 9)

Substitute x = 2 into f(x):

`\implies f(2)=2(2)+5=9`

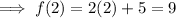
Substitute x = 9 into g(x):

`\implies g(9)=(9-5)/(2)=2`

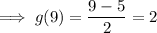
Therefore, the functions are inverses of each other since the x-value of function f equals the y-value of function g, and the y-value of function f equals the x-value of function g.