Question

The cubic polynomial x ^3 - 3x ^ 2 + ax + b is factor (x - 2)

(a)Find a linear relationship between a and b (b )Find the remainder when the polynomial is divided by
(a)(x-1)
(b)x-3)

Answer 1

Answer: Look at step-by-step explanation

Explanation:

1) When a polynomial f(x) has a factor x - y, then f(y) = 0, hence

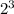`2^(3)` - 3 ×
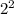`2^(2)` + 2a + b = 0

8 - 12 + 2a + b = 0

2a + b = 4

2) When a polynomial f(x) is divided by x - y, then f(y) = the remainder, hence

(A) When divided by x - 1

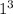`1^(3)` - 3 ×
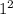`1^(2)` + a + b = 1 - 3 + a + b = a + b - 2

(B) When divided by x - 3

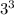`3^(3)` - 3 ×
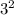`3^(2)` + 3a + b = 27 - 27 + 3a + b = 3a + b