to get the slope of any straight line, we simply need two points off of it, let's use those in the picture below.
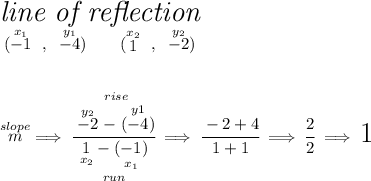
now, keeping in mind that perpendicular lines have negative reciprocal slopes, there are three dotted lines, each one of them, hits the line of reflection perpendicularly, so their slope must be
