Question

How much would you need to deposit in an account now in order to have $5000 in the account in 5 years? Assume the account earns 5% interest compounded daily.

Answer 1

$3893.97

Explanation:

5000 = x (1 + 0.05/365)^365 * 5

5000 = x ( 1 + 0.000137)^1825

5000 = x (1.000137)^1825

5000 = 1.284036 x

1.284036 / 1.284036 x = 5000 / 1.284036

x = 3 893.97182

x = 3 893.97

Answer 2

$3,894.07

Explanation:

`\boxed{\begin{minipage}{8.5 cm}\underline{Compound Interest Formula}\\\\$ A=P\left(1+(r)/(n)\right)^(nt)$\\\\where:\\\\ \phantom{ww}$\bullet$ $A =$ final amount \\ \phantom{ww}$\bullet$ $P =$ principal amount \\ \phantom{ww}$\bullet$ $r =$ interest rate (in decimal form) \\ \phantom{ww}$\bullet$ $n =$ number of times interest is applied per year \\ \phantom{ww}$\bullet$ $t =$ time (in years) \\ \end{minipage}}`

Given:

• A = $5,000
• r = 5% = 0.05
• n = 365 (daily)
• t = 5 years

Substitute the given values into the formula and solve for P:

`\implies 5000=P\left(1+(0.05)/(365)\right)^(365 * 5)`

`\implies 5000=P\left(1.000136986...\right)^(1825)`

`\implies P=(5000)/(\left(1.000136986...\right)^(1825))`

`\implies P=3894.070588...`

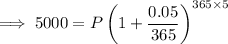
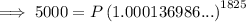
Therefore, the amount you would need to deposit in an account now in order to have $5,000 in the account in 5 years time is $3,894.07.