Answer:
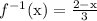
===============================================
Work Shown:
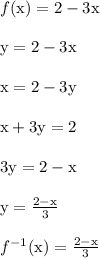
-----------------
Explanation:
The process to find the inverse involves this outline.
- Replace f(x) with y.
- Swap x and y.
- Solve for y.
This process is followed in the "work shown" portion above.
To confirm the answer, let g(x) be the inverse of f(x).
If they were inverses of each other, then these two properties would hold true:
- f( g(x) ) = x
- g( f(x) ) = x
Here's the verification for the first part.
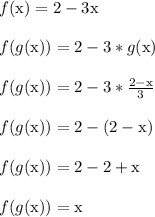
I'll let you do the other confirmation.