Answer:
The ball will take approximately 2.165 seconds.
Explanation:
The height of the ball is represented by the function
 , the time taken by the ball to hit the ground is a value of
, the time taken by the ball to hit the ground is a value of
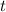 such that
such that
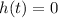 , we proceed to solve the following equation for
, we proceed to solve the following equation for
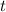 :
:
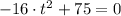 (1)
(1)
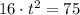
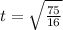
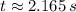
The ball will take approximately 2.165 seconds.