Answer:
Approximately
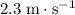 to the left.
to the left.
Step-by-step explanation:
When an object of mass
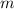 travels at a velocity of
travels at a velocity of
 , the momentum
, the momentum
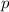 of that object will be
of that object will be
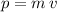 .
.
Denote motions to the right with a positive sign.
Before the collision:
- Velocity of the canoe was
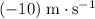 since the canoe was moving to the left (opposite to the positive direction.) Momentum of the canoe was
since the canoe was moving to the left (opposite to the positive direction.) Momentum of the canoe was
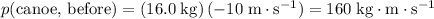 .
. - Velocity of the raft was
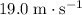 since the raft is moving to the right (towards positive direction.) Momentum of the raft was
since the raft is moving to the right (towards positive direction.) Momentum of the raft was
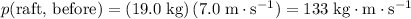 .
.
After the collision:
- Velocity of the canoe becomes
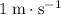 (to the right, towards the positive direction.) Momentum of the canoe becomes
(to the right, towards the positive direction.) Momentum of the canoe becomes
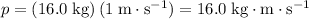 .
. - Velocity of the raft after the collision needs to be found.
Immediately after the collision, momentum
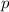 of the canoe and the raft will be conserved. In other words:
of the canoe and the raft will be conserved. In other words:
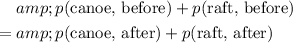 .
.
Rearrange to find
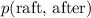 (momentum of the raft immediately after the collision.)
(momentum of the raft immediately after the collision.)
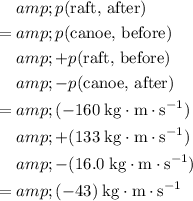 .
.
(Momentum of the raft is negative since the raft is moving to the left, away from the positive direction.)
Divide the momentum of the raft by the mass of the raft to find the velocity of the raft:
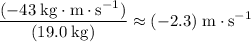 .
.