Answer:
(a) Other zeros: 3i and -4-i
(b) 9
(c) 10
Explanation:
Given information:
- Polynomial function with real coefficients.
- Degree: 13
- Zeros: 2, -4, 3i, -4+i
Part (a)
For any complex number
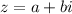 , the complex conjugate of the number is defined as
, the complex conjugate of the number is defined as
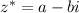 .
.
If f(z) is a polynomial with real coefficients, and z₁ is a root of f(z)=0, then its complex conjugate z₁* is also a root of f(z)=0.
Therefore, if R(x) is a polynomial with real coefficients, and 3i is a root of R(x)=0, then its complex conjugate -3i is also a root of R(x)=0.
Similarly, if -4+i is a root of R(x)=0, then its complex conjugate -4-i is also a root of R(x)=0.
Part (b)
The degree of the polynomial is the greatest of the exponents of its various terms.
The degree of R(x) with just the given roots (including the complex conjugates) is 6, which includes 2 real zeros.
As the actual degree of R(x) is 13, the maximum number of real zeros would be 7 more than the given real zeros.
Therefore, the maximum number of real zeros that R(x) can have is 9.
Part (c)
For each complex root there is also a complex conjugate root.
We have been given 2 complex zeros and 2 real roots, so when we include the complex conjugates, the degree of R(x) is 6.
The actual degree of R(x) is 13, so the maximum number of non-real zeros is 6 more (as they come in pairs) than the already given 4 non-real zeros. Therefore, the maximum number of non-real zeros that R(x) can have is 10.