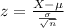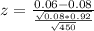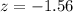Answer:
The correct value of the Z-statistic is z = -1.56
Explanation:
A company manufacturing computer chips finds that 8% of all chips manufactured are defective.
This means that the null hypothesis is:
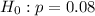
A hypothesis test is performed to determine if the additional training was effective in lowering the defect rate.
This means that the alternate hypothesis is:
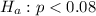
z-statistic:
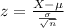
In which X is the sample mean,
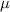 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
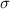 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
0.08 is tested at the null hypothesis:
This means that
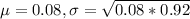
After training was implemented, a sample of 450 chips revealed only 27 defects.
This means that
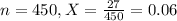
The correct value of the Z-statistic is