Question

The tablets were crushed, and 4.9993 g of the powder was transferred to a beaker and reacted with HCl. After filtration, the filtrate was transferred to a 100-mL volumetric flask and diluted with water. 20.00 mL of this stock solution were combined with 0.2 M Na3PO4. The resulting precipitate weighed 0.3451 g after drying. Calculate the moles of BiPO4 precipitated, the moles of Bi3 in the stock solution, and the mass of BSS per tablet.

Answer 1

Step-by-step explanation:

From the information given:

Mass of BiPO₄ = 0.3451 g

Number of moles of BiPO₄ =
`0.3451 \ g \ BiPO_4 * (1 \ mol \ BiPO_4)/(303.95 \ g \ BiPO_4)`

`= 0.001135 \ mol`

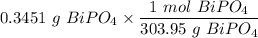
The number of moles of Bi³⁺ in 20.00 mL is:
`= 0.001135 \ mol \ BiPO_4 * (1 \ mol \ of \ Bi^(3+))/(1 \ mol \ BiPO_4)`

= 0.001135 mol of Bi³⁺

The number of moles of Bi³⁺ in 100 mL stock solution

`= 0.001135 \ mol \ Bi^(3+) * (100 \ mL)/(20.0 \ mL)`

`= 0.005675 \ mol`

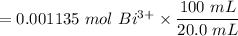
Mass of BSS in 4.9993 g tablets

`m = 0.005675 \ mol \ Bi^(3+) * (1 \ mol \ BSS)/(1 \ mol \Bi^(3+)) * (362.1 \ g \ BSS)/(1 \ mol \ BSS)`

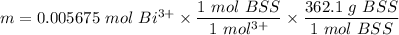
m = 2.055 g BSS

Mass of BSS in 5.0103 g (5 tables)

`m = 2.055 g \ BSS * (5.0103 \ g)/(4.9993 \ g)`

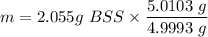
= 2.06 g

∴

The mass of BSS per tablet is
`=(2.06 \ g)/(5 \ tablet)`

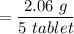
= 0.412 g BSS/ tablet