Answer:
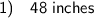
![\textsf{2)\quad$2\sqrt[3]{3}$\; inches}](https://img.qammunity.org/2023/formulas/mathematics/high-school/dx4mnfc4057ku97b0ca70wa81l5cihusy5.png)
Explanation:
Question 1
Define the variables:
- Let x be the length of the string.
- Let y be the rate of vibration of a string under constant tension.
The rate of vibration of a string under constant tension varies inversely with the length of the string:
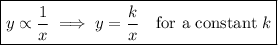
Given values:
- x = 24 inches
- y = 128 times per second
Substitute the given values of x and y into the formula and solve for k:

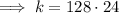
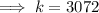
Therefore, the equation is:
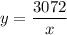
To find the length of a string that vibrates 64 times per second, substitute y = 64 into the equation and solve for x:
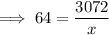
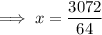
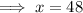
Therefore, the length of a string that vibrates 64 times per second is 48 inches.
---------------------------------------------------------------------------------------------
Question 2
Define the variables:
- Let y be the horsepower (hp) that a shaft can safely transmit.
- Let v be the speed of the shaft (in rpm).
- Let d be the diameter of the shaft (in inches).
The horsepower that a shaft can safely transmit varies jointly with its speed and the cube of the diameter:
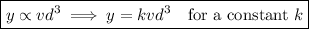
Given values:
- y = 45 hp
- v = 100 rpm
- d = 3 inches
Substitute the given values of y, v and d into the formula and solve for k:
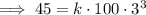
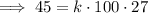
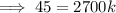
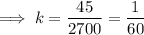
Therefore, the equation is:
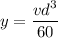
To find the diameter of the shaft in order to transmit 60 hp at 150 rpm, substitute y = 60 and v = 150 into the equation and solve for d:

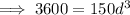
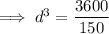

![\implies d=\sqrt[3]{24}](https://img.qammunity.org/2023/formulas/mathematics/high-school/4wen9epnm1gm3szr3wv31ydrq4zji4422w.png)
![\implies d=\sqrt[3]{8 \cdot 3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/sjkssc65cnuy3xf63zp4k8gqpm8k5z06i2.png)
![\implies d=\sqrt[3]{8} \sqrt[3]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/nuc7y8jn2xf3fhlhgreduf9q3qlkss5o49.png)
![\implies d=\sqrt[3]{2^3} \cdot \sqrt[3]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/fuguv8j0jwesw1o96teaw7fhyzr1dejbz9.png)
![\implies d=2\sqrt[3]{3}](https://img.qammunity.org/2023/formulas/mathematics/high-school/r5rulq7pv1giniu7dyn51yu8j13ij0qctp.png)
Therefore, the diameter of a shaft that transmits 60 hp at 150 rpm is 2³√3 inches.