Question

Pls help need help ASAP 50 points you will be reported if the answer is wrong Pls help need help ASAP 50 points you will be reported if the answer is wrong

Answer 1

4*1.5=6
3*4=12
3*4*(1/2)=6
=24cm^2

Answer 2

`\Huge\boxed{24cm^2}`

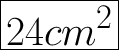
Explanation:

Hello There!

The following figure shown is a composite figure (meaning we can't find the area of it using one formula)

So in order to find the total area we are going to want to split the figure into 3 shapes

A rectangle with a width of 3 and a length of 4 (found by subtracting the total length of the composite figure by the triangles length 8-4=4 so the length of the rectangles are 4 cm

Another rectangle with a width of 1.5 and a length of 4 ( once again found by subtracting the total length of the composite figure by the triangles length 8-4=4 so the length of the rectangles are 4 cm )

And a triangle with a height of 4 and a base of 3

Now lets find the area of each individual shape

for rectangle #1

The area of a rectangle can easily be calculated by multiplying the length and width

so A = 3 x 4

3 x 4 = 12 so the area of the larger rectangle is 12 cm^2

for rectangle #2 Once again the area of a rectangle can simply be found my multiplying the length and the width

So A = 1.5 x 4

1.5 * 4 = 6 so the area of the smaller rectangle is 6 cm^2

For the triangle

We can solve for the area of a triangle using this formula

`A=(bh)/(2)`

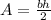
where b = base and h = height

we already know the length of the base and height so all we have to do is plug in the values into the formula

so

`A=(4*3)/(2) \\4*3=12\\(12)/(2) =6`

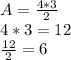
So the area of the triangle is 6 cm ^2

finally we want to add all of the areas together

6 + 6 + 12 = 24

So the total area of the composite figure is 24 cm ^2