Question

Prove: The opposite sides of a parallelogram are equal.

Answer 1

A=(0,0), B=(b,0), C=(b+c,d), D=(c,d) Then Using the distance formula

DC=√(c-[b+c])2+(d-d)2 DC=√b2 DC=b AB=√(0-b)2+(0-0)2 AB=√(-b)2 AB=√b2 AB=b then DC=AB DA=√(c-0)2+(d-0)2 DA=√c2+d2 CB=√(b+c-b)2+(d-0)2 CB=√c2+d2 then DA=CB

Explanation:

Answer 2

Since AD = BC and AB = CD, the opposite sides of parallelogram ABCD are equal, proving the property of a parallelogram.

The figure includes a parallelogram ABCD with vertices A at (0,0), B at (b,0), C at (b+c,a), and D at (c,a). The proof for the opposite sides of a parallelogram being equal typically involves showing that the distances between corresponding vertices are the same.

Here's the general approach to the proof, using the distance formula for points in the plane:

1. Distance Formula: The distance between any two points
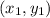`\( (x_1, y_1) \)` and
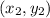`\( (x_2, y_2) \)` in the plane is given by the formula

`\[ d = √((x_2 - x_1)^2 + (y_2 - y_1)^2) \]`

2. Calculate AD and BC: To show that AD and BC are equal, calculate the distance between A and D and the distance between B and C using the distance formula.

• AD = Distance between A(0,0) and D(c,a) =
  `\( √((c - 0)^2 + (a - 0)^2) \)`
• BC = Distance between B(b,0) and C(b+c,a) =
  `\( √(((b+c) - b)^2 + (a - 0)^2) \)`

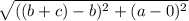
3. Calculate AB and CD: To show that AB and CD are equal, calculate the distance between A and B and the distance between C and D using the distance formula.

• AB = Distance between A(0,0) and B(b,0) =
  `\( √((b - 0)^2 + (0 - 0)^2) \)`
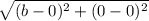
• CD = Distance between C(b+c,a) and D(c,a) =
  `\( √((c - (b+c))^2 + (a - a)^2) \)`

4. Compare the Distances: After calculating the distances, you'll see that AD and BC are equal because they both simplify to
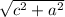`\( √(c^2 + a^2) \)`, and AB and CD are equal because they both simplify to
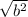`\( √(b^2) \)`.