Explanation:
Given - In selecting a sulfur concrete for roadway construction in regions that experience heavy frost, it is important that the chosen concrete has a low value of thermal conductivity in order to minimize subsequent damage due to changing temperatures. Suppose two types of concrete, a graded aggregate and a no-fines aggregate, are being considered for a certain road. The table below summarizes data on thermal conductivity from an experiment carried out to compare the two types of concrete.
Type ni xi si
Graded 42 0.486 0.187
No-fines 42 0.359 0.158
To find - a. Formulate the above in terms of a hypothesis testing problem.
b. Give the test statistic and its reference distribution (under the null hypothesis).
c. Report the p-value of the test statistic and use it to assess the evidence that this sample provides on the scientific question of difference in mean conductivity of the two materials at the 5% level of significance.
Proof -
a.)
Hypothesis testing problem :
H0 : There is significant difference between mean conductivity for the graded concrete and mean conductivity for the no fines concrete.
H1 : There is no significant difference between mean conductivity for the graded concrete and mean conductivity for the no fines concrete.
b)
Test statistic :
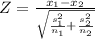
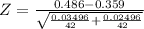
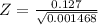
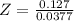
⇒Z(cal) = 3.3687
Z(tab) = 1.96
As Z (cal) > Z(tab)
So, we reject H0 at 5% Level of significance
p-value = 0.99962
Hence
There is significant difference in mean conductivity at the two materials.