Question

Determine the enthalpy of neutralization in Joules/mmol for a solution resulting from 19 mL of 1 M NaOH solution and 19 mL of a HCl with the same molarity. If separately, each had a temperature of 28.6 degrees Celsius, and upon addition, the highest temperature reached by the solution was graphically determined to be 37.3 degrees Celsius. Round to the nearest whole number.

Answer 1

`\Delta _(neutralization)H=-73(J)/(mmol)`

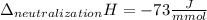
Step-by-step explanation:

Hello there!

In this case, by considering this calorimetry problem, it is possible to realize that the heat released by the reaction between HCl and NaOH is absorbed by the reaction mixture, which can be assumed to have the same density and specific heat of pure water; thus, we calculate this heat as a function of the specified temperature change:

`Q_(rxn)=-Q_(solution)\\\\Q_(rxn)=-m_(solution)C_(solution)(T_2-T_1)`

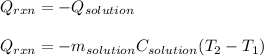
Thus, we plug in the data, by also considering that the total volume of solution is 19mL+19mL=38mL:

`Q_(rxn)=-(38mL*(1g)/(1mL) )(4.184(J)/(g\°C)) (37.3\°C-28.6\°C)\\\\Q_(rxn)=-1383.2J`

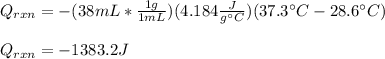
Next, since the reaction between NaOH and HCl is:

`NaOH+HCl\rightarrow NaCl+H_2O`

Whereas there is 1:1 mole ratio of NaOH to HCl, we infer they both react with the same moles, defined by the volume and molarity:

`n_(rxn)=0.019L*1mol/L\\\\n_(rxn)=0.019mol`

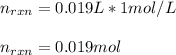
Finally, to compute the enthalpy of neutralization we divide the total heat due to the reaction by the reaction moles to obtain:

`\Delta _(neutralization)H=(Q_(rxn))/(n_(rxn)=)\\\\ \Delta _(neutralization)H=(-1383.23J)/(0.019mol)\\\\\Delta _(neutralization)H=-72801.6(J)/(mol)*(1mol)/(1000mmol)\\\\\Delta _(neutralization)H=-73(J)/(mmol)`

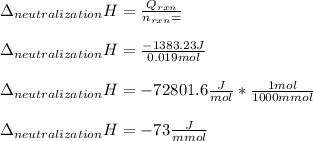
Best regards!