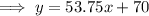Question

Please help I need detailed explication. I will give 100 points and brianliest.

Write a linear equation that represents the trend line that you have drawn. Be sure to use points that are located on your trend line to find the equation. Show your work.

Answer 1

`y=53.75x+70`

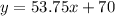
Explanation:

From inspection of the given graph with added trendline:

• y-intercept ≈ (0, 70)
• another point on the trendline ≈ (8, 500)

Find the slope of the trendline by substituting the identified points into the slope formula:

`\implies \textsf{slope}\:(m)=(y_2-y_1)/(x_2-x_1)=(500-70)/(8-0)=53.75`

`\boxed{\begin{minipage}{6.3 cm}\underline{Slope-intercept form of a linear equation}\\\\$y=mx+b$\\\\where:\\ \phantom{ww}$\bullet$ $m$ is the slope. \\ \phantom{ww}$\bullet$ $b$ is the $y$-intercept.\\\end{minipage}}`

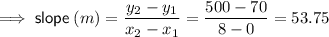
Substitute the found slope and y-intercept into the slope-intercept formula to create an equation for the trendline:

`\implies y=53.75x+70`