Answer:
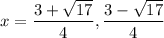
Explanation:
The quadratic formula is a method of solving for x in a quadratic function.
Quadratic Formula
Remember that quadratic functions are written as ax^2 + bx + c. The quadratic formula is
 and is used when the function is equal to 0. So, for this function: a = 2, b = -3, and c = -1.
and is used when the function is equal to 0. So, for this function: a = 2, b = -3, and c = -1.
Solving For x
That means the quadratic formula will look like
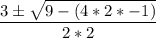 . To find x, first, we can simplify the denominator.
. To find x, first, we can simplify the denominator.
Next, we can first solve the expression under the square root.
Then, since this is not a perfect square, we can just put this back into the equation to get the final answer.