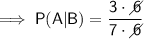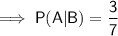Answer:
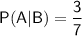
Explanation:
The general equation for conditional probability is:

Given probabilities:
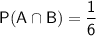
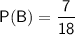
Substitute the given probabilities into the equation and solve for P(A|B).
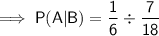
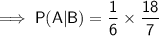
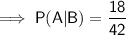
Reduce the fraction to its simplest form by dividing the numerator and denominator by 6: