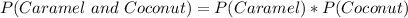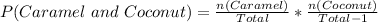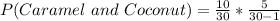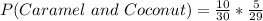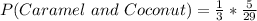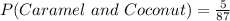Question

selects a piece of candy and eats it (so it is NOT replaced!) Then selects a piece of candy and eats it. Find the probability of each event

Answer 1

Question:

There are 30 candies in a box, all identically shaped. 5 are filled with coconut, 10 with caramel, and 15 are solid chocolate.

You randomly select a piece of candy and eat it (so it is NOT replaced!), then select a second piece. Find the probability of each event

(a) The probability of selecting two solid chocolates in a row.

(b) The probability of selecting a caramel and then a coconut candy.

Answer:

`(a)`
`P(Chocolates) = (7)/(29)`

`(b)`
`P(Caramel\ and\ Coconut) = (5)/(87)`

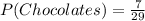
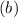
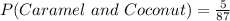
Explanation:

Given

`Coconut = 5`

`Caramel = 10`

`Chocolate = 15`

`Total = 30`

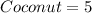
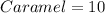
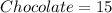
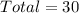
For probabilities without replacement, 1 is subtracted after the first selection.

So, we have:

Solving (a): Two solid chocolates

This is calculated as:

`P(Chocolates) = P(First\ Chocolate) * P(Second\ Chocolate)`

`P(Chocolates) = (n(Chocolate))/(Total) * (n(Chocolate) - 1)/(Total - 1)`

`P(Chocolates) = (15)/(30) * (15 - 1)/(30 - 1)`

`P(Chocolates) = (15)/(30) * (14)/(29)`

`P(Chocolates) = (1)/(2) * (14)/(29)`

`P(Chocolates) = (7)/(29)`

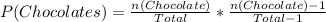
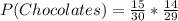
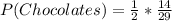
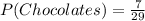
Solving (a): Caramel and Coconut

This is calculated as:

`P(Caramel\ and\ Coconut) = P(Caramel) * P(Coconut)`

`P(Caramel\ and\ Coconut) = (n(Caramel))/(Total) * (n(Coconut))/(Total - 1)`

`P(Caramel\ and\ Coconut) = (10)/(30) * (5)/(30- 1)`

`P(Caramel\ and\ Coconut) = (10)/(30) * (5)/(29)`

`P(Caramel\ and\ Coconut) = (1)/(3) * (5)/(29)`

`P(Caramel\ and\ Coconut) = (5)/(87)`