( 2 ,6.5 ) lied on the parabola which mean when we put the x=2 in the equation the y value would be 6.5 :
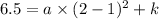
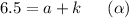
In the otherhand ( -1 , - 1 ) has the same condition:
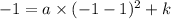

_____________________________________________
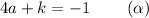

Multiply Beta by (-1) :
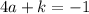

then we have to find the submission of alpha and beta :
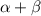
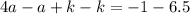
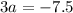
Divide both sides by 3
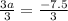

Put the value of a in one of the above equations to find the value of k .I'm gonna use the second equation ( beta ) :
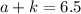
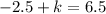
Add both sides by 2.5
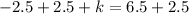
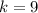
Thus the equation of the parabola is :
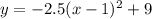
The maximum value of the parabola is for the vertex which is x = 1 , so we have to put it in the equation and find it's y coordinate :
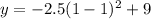
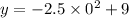
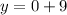

Adn we're done ...