Question

If the value of x must be an integer, what is the length of the left side of the large triangle?

Answer 1

Maybe 6 2/3 (see below); there is definitely something wrong with the figure.

Explanation:

Because of the marked congruent angles, and the shared angle, the two triangles are similar by AA. Therefore,

`(x-1)/(x)=(3x+1)/(6)`

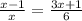
6(x-1) = x(3x+1)

6x - 6 = 3x² + x

3x² - 5x + 6 = 0

Not factorable, so x can't be an integer.

BUT, if we change (x-1) to (2x-1), it's doable!!

`(2x-1)/(x)=(3x+1)/(6)`

6(2x-1) = x(3x+1)

12x - 6 = 3x² + x

3x² - 11x + 6 = 0

3x-2 = 0 ⇒ x=2/3 (not a solution to this particular problem);

x-3 = 0 ⇒ x=3

Plugging x=3 into 3x+1 = 3(3)+1 = 10

So,
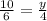`(10)/(6)=(y)/(4)` ⇒ 3y = 20 ⇒ y = 20/3 or 6 2/3