Question

↓

10 cm
to
16 cm
The area of the triangle is 55cm²
Work out the value of x.
Give your answer to 1 decimal place.

Answer 1

x = 43.4°

Explanation:

Given a triangle with two sides, say a and b and the included angle, x, the area can be directly determined using the formula

`Area = (1)/(2) \cdot a \cdot b \cdot sin(x)`

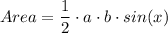
Here we are not given x but we can work backward since we are given area = 55, side a = 10, side b = 16

Plug in values for knowns:

`55= (1)/(2) \cdot 10 \cdot 16 \cdot sin(x)`

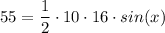
55 = 80 sin(x)

Switch sides

80 sin(x) = 55

Divide both sides by 80

==> sin(x) = 55/80 = 0.6875

==> x = sin⁻¹(0.6875)

x = 43.4325°

To one decimal place this would be

x = 43.4°

Hope that helps