The original price of the car when it was new was approximately $2,160.84.
The formula for exponential depreciation is given by:
![\[ P(t) = P_0 \cdot e^(rt) \]](https://img.qammunity.org/2023/formulas/mathematics/college/6z78vhqcduzz908s56fumto7xep3kgymeq.png)
Where:
-
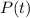 is the current value of the asset at time
is the current value of the asset at time
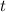 ,
,
-
 is the original value of the asset,
is the original value of the asset,
-
 is the annual depreciation rate (expressed as a decimal),
is the annual depreciation rate (expressed as a decimal),
-
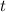 is the time in years,
is the time in years,
-
 is the mathematical constant approximately equal to 2.71828.
is the mathematical constant approximately equal to 2.71828.
In this case, the car is 8 years old, the current value is $6,700, and the depreciation rate is 14.15% per year.
Let's substitute these values into the formula:
![\[ 6700 = P_0 \cdot e^((0.1415 \cdot 8)) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/xc8zbii6wxr6oyrdpc49c8iti09rjz4b85.png)
Now, solve for
 , the original price:
, the original price:
![\[ 6700 = P_0 \cdot e^(1.132) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/gqxjttqatihjw8a11bu44n5fkdiw11ahsu.png)
To solve for
 , divide both sides by
, divide both sides by
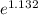 :
:
![\[ P_0 = (6700)/(e^(1.132)) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/25hkns57y0idgvcaxfpfxzz343fvatkb0s.png)
Using a calculator:
![\[ P_0 \approx (6700)/(e^(1.132)) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/5g5ouipsgsxn406ge8wc4arddnpnli6op5.png)
![\[ P_0 \approx (6700)/(3.1009) \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/9yahknp3qshb4maoehbms78qsif26utlpq.png)
![\[ P_0 \approx 2160.84 \]](https://img.qammunity.org/2023/formulas/mathematics/high-school/6udtcoceo8r6v1lz47ednfbuoti7anlo8p.png)
Therefore, the original price of the car when it was new was approximately $2,160.84.