Question

Please help! i’ll give points

Answer 1

∠SQA=45°, ∠QRU=90°, ∠QSA=90°, RU≈7.0711 (round as needed), and UA=10

Explanation:

Squares are the last shape on the quadrilateral family tree, meaning they inherit many properties. An image is attached to show the tree.

∠SQA=45° because the diagonals of a square cut the angles of the square in half. This is also known as an angle bisector. This property is inherited from the rectangle properties.

∠QRU=90° because the diagonals form 4 right isosceles triangles. This property is inherited from the rhombus.

∠QSA=90° because each of the outer edges forms a right angle.

The length of RU can be determined using Pythagorean Theorem. Pythagorean Theorem states that
`a^2+b^2=c^2`, where a and b are the sides of a right triangle and c is the hypotenuse (the side opposite the right angle). Looking at ΔSUA, a and b are both 10 because all of the sides of a square are equal. Therefore
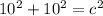`10^2+10^2=c^2`, 100+100=
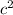`c^2`, 200=
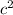`c^2`, c≈14.1421, c/2≈7.0711. R≈7.0711

UA is 10 because all the sides of a square are equivalent.

Answer 2

SQA=45

QRU=90

QSA=90

RU=5 because SU = 10

UA=2
`√(5)`

RU=5 and RA = 5

If you make a 5 x 5 square, do pythagorean theorem to find c^2. You get
`√(50)`. Simplify that further to my answer for UA.