Question

Two English classes with the same number of students took a final exam.

The box-and-whisker plots below (sometimes called boxplots) summarize the test scores for each class.
Use the box-and-whisker plots to answer the questions.

Answer 1

(a): Class A

(b): Class B

(c): class A

(d): Class B

Explanation:

Box-and-Whisker plot

A box-and-whisker plot shows us 5 key values in a data set: minimum, quartile one, median, quartile three, and maximum.

the first point on the far left is the minimum value, the second point which is going to be on the left side of the box is the quartile one this is going to be at the 25th percentile, the third point which is going to be inside the box is the median which is at the 50th percentile or middle of the data set, and the fourth point is going to be on the right side of the box which is quartile three and is going to be at the 75th percentile and finally on the far right you're going to have the maximum value.

We can define some values knowing these five values:

`\text{Interquartile Range} = Q_3 - Q_1\\\text{Range} = \text{Maximum} - \text{Minimum}`

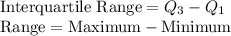
Visually the range is just how seperated the values are. The interquartile range is similar to the range, except it's the width of the box, or distance between the quartile 1 and 3 and is a good way for measuring spread in some cases.

Visually it's obvious that class A has a wider IQR, since the box is wider.

The median score is the point in the box, and class B has this point more farther on the right than class A

Class A has the last point farther to the right, which represents the maximum value in this data set, so class A had the highest test score.

class B has less distance between the two end points, so they have a smaller range/