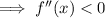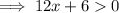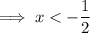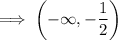Answer:
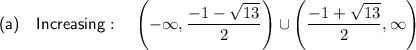
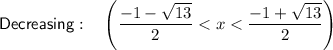
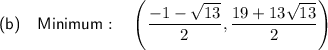
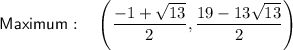



Explanation:
Given function:
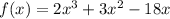
Part (a)

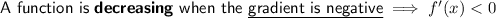
Differentiate the given function:
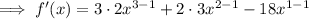

Complete the square:
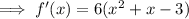
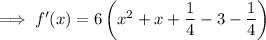

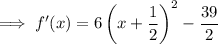
Increasing
To find the interval where f(x) is increasing, set the differentiated function to more than zero:
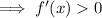
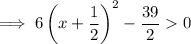
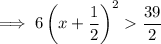
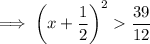
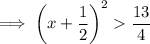
![\textsf{For\;\;$u^n > a$,\;\;if\;$n$\;is\;even\;then\;\;$u < -\sqrt[n]{a}$\;\;or\;\;$u > \sqrt[n]{a}$}.](https://img.qammunity.org/2023/formulas/mathematics/college/uugkvfcdl4sk9rp4ou2xh1q9t6mgjehzdl.png)
Therefore:
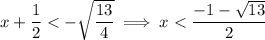
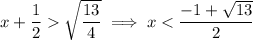
So the interval on which function f(x) is increasing is:
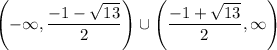
Decreasing
To find the interval where f(x) is decreasing, set the differentiated function to less than zero:
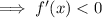
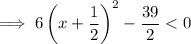

![\textsf{For\;\;$u^n < a$,\;\;if\;$n$\;is\;even\;then\;\;$-\sqrt[n]{a} < u < \sqrt[n]{a}$}.](https://img.qammunity.org/2023/formulas/mathematics/college/jho0ze5f58r9xmve9hyc28o6b7rz7pqm9y.png)
Therefore:
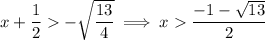
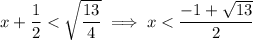
So the interval on which function f(x) is decreasing is:
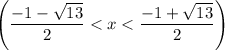
Part (b)
To find x-coordinates of the local minimum and maximum set the differentiated function to zero and solve for x:
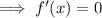
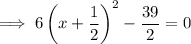
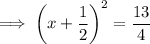
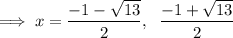
To find the y-coordinates of the turning points, substitute the found values of x into the function and solve for y:
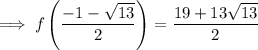
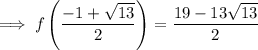
Therefore:
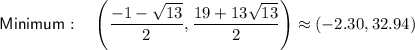
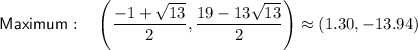
Part (c)
At a point of inflection, f''(x) = 0.
To find the point of inflection, differentiate the function again:
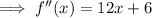
Set the second derivative to zero and solve for x:
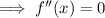
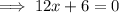
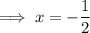
Substitute the found value of x into the original function to the find the y-coordinate of the point of inflection:
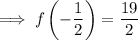
Therefore, the inflection point is:
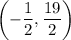
A curve y = f(x) is concave up if f''(x) > 0 for all values of x.
A curve y = f(x) is concave down if f''(x) < 0 for all values of x.
Concave up
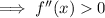
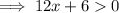
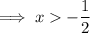

Concave down