Question

What is the exact area of triangle ABC? show all work

The triangle has a 30-degree angle at C, 24m at CB, and a 90-degree angle at B

Answer 1

96√3

Explanation:

Answer 2

96√3 m²

Explanation:

Triangle ABC is a 30-60-90 triangle.

This is a special right triangle where the measures of its sides are in proportion
`x:x√(3):2x`:

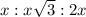• x is the side opposite the 30° angle
• x√3 is the side opposite the 60° angle.
• 2x is the side opposite the right angle.

The side opposite the 30° angle is the height of the triangle.

The side opposite the 60° angle is the base of the triangle and is 24 m.

Therefore, find x:

`\implies x√(3)=24\\\\ \implies x=(24)/(√(3))\\\\ \implies x=8√(3)`

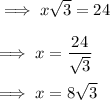
Therefore:

• Base of the triangle = 24 m
• Height of the triangle = 8√3 m

`\boxed{\begin{minipage}{4 cm}\underline{Area of a triangle} \\\\$A=(1)/(2)bh$\\\\where:\\ \phantom{ww}$\bullet$ $b$ is the base. \\ \phantom{ww}$\bullet$ $h$ is the height. \\\end{minipage}}`

Substitute the found base and height into the formula and solve for area:

`\implies A=(1)/(2) \cdot 24 \cdot 8√(3)`

`\implies A=12 \cdot 8√(3)`

`\implies A=96√(3)\;\; \sf m^2`

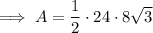
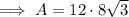
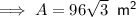
Therefore, the exact area of the triangle is 96√3 m².