Question

Tom and his little sister are enjoying an afternoon at the ice rink. They playfully place their hands together and push against each other. Tom's mass is 76 kg and his little sister's mass is 15 kg.

(a) Which of the following statements is correct?
They both experience the same force.The force experienced by Tom is less than the force experienced by his sister. The force experienced by the sister is less than the force experienced by Tom.
(b) Which of the following statements is correct?
Tom's acceleration is more than the sister's acceleration.Tom's acceleration is less than the sister's acceleration. They both have the same acceleration.
(c) If the sister's acceleration is 2.3 m/s2 in magnitude, what is the magnitude of Tom's acceleration?
m/s2

Answer 1

Tom and his sister experience a net force of the same magnitude.

The acceleration of Tom is less than that of his sister.

The magnitude of the acceleration of Tom will be approximately
`0.45\; {\rm m\cdot s^(-2)}`.

Step-by-step explanation:

Assume that friction is negligible and that the ice rink is level. The only unbalanced force on Tom will be the force from his sister.

By Newton's Laws of Motion, Tom's sister will experience a reaction force from Tom. This reaction force will be equal in magnitude to the force on Tom, but opposite in the direction.

If friction is negligible and the rink is level, the net force on Tom will be equal to that on his sister. However, acceleration is inversely proportional to mass: if the net force on an object is
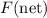`F(\text{net})` and the mass of the object is
`m`, the acceleration
`a` of that object will be
`a = (F(\text{net})) / m`.

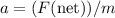Since Tom's mass is greater than that of his sister and the magnitude of net force on them is the same, the acceleration of Tom's sister will be greater.

Using the equation
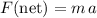`F(\text{net}) = m\, a`, find the magnitude of the net force on Tom's sister:

`\begin{aligned}F(\text{net, sister}) &= m(\text{sister})\, a(\text{sister}) \\ &= (15\; {\rm kg}) \, (2.3\; {\rm m\cdot s^(-2)})\\ &= 34.5\; {\rm N}\end{aligned}`.

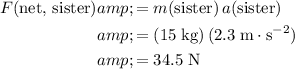Since the net force on Tom is the same as that on his sister, the magnitude of the net force on Tom will also be
`34.5\; {\rm N}`. Since the mass of Tom is
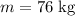`m = 76\; {\rm kg}`, the acceleration of Tom will be:

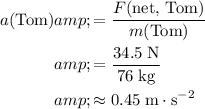`\begin{aligned}a(\text{Tom}) &= \frac{F(\text{net, Tom})}{m(\text{Tom})} \\ &= \frac{34.5\; {\rm N}}{76\; {\rm kg}} \\ &\approx 0.45\; {\rm m\cdot s^(-2)}\end{aligned}`.