Answer:
x= 37 , y= 143
Explanation:
okay so to start out we must write an equation in order to find the angles of a parallelogram.
2x+2y=360 (the angles of a parallelogram always equal 360 degrees)
next, since we know that the angle for y is "y+3" we can substitute this into the equation
2x+2(y+3)=360
next, since it is given that y=3x+29 we can now substitute that into the equation
2x+2[(3x+29)+3]=360
now, SOLVE!
![2x+2[(3x+29)+3]=360 \\2x+2(3x+32)=360 \\2x+6x+64=360\\8x+64=360\\8x=296\\x=37](https://img.qammunity.org/2023/formulas/mathematics/high-school/9u22zpcm409chfwr2wywqab5223m75r2p5.png)
okay, now we know that x=37 degrees so now we must find y. this can be done by substituting 37 into (3x+29)+3 or simply, 3x+32
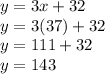
don't forget to check your work!
2(37)+2(143)=360
there you go! so x= 37 degrees and y= 143 degrees