Given equation to us is ,
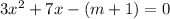 .
.
The given equation is a quadratic equation and it has two real solutions if it's discriminant is greater than or equal to 0 .
For a quadratic equation in standard form of
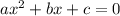
the discriminant is given by b² - 4ac .
On comparing wrt to Standard form, we have ;
Hence we have,

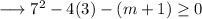
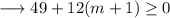
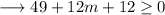
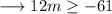

Therefore the given quadratic equation will have real solutions for values of m greater than or equal to -61/12 .
And we are done!